Group 21 Spotify Project
Matthew Finney • Kaivalya Rawal • Royce Yap • David Zheng
Naive Bayes Classifier
Based upon the EDA conducted, we had a feeling that individual song features add little information to the music recommendation solution. Further, to model a real world setting, we would wish a model that might be slow to fit initially (train), but is extremely fast to execute later (predict from). With these two considerations in mind, we propose to use a Naive-Bayes model to classify songs as belonging to a playlist recommendations or not.
Theory
A naive Bayes classifier is a probabilistic classification model that encodes a belief about independences in the features. Specifically, the naive Bayes classifier assumes that each feature is conditionally independ of every other feature, given the class of the response:
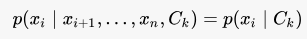
Armed with this assumption, naive Bayes uses the familiar Bayes rule to predict the probability of the response variable belonging to a particular class.
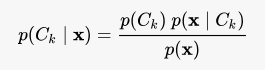
Thus, the final form of the prediction function in the case of naive Bayes is:
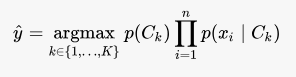
All formula images sourced from Wikipedia.
Implementation
As mentioned above, we wished to explore the creation of a recommender system that did not require the explicit use of various song features. Thus, the problem can be cast as consisting of a prediction function that takes the 70% of the songs in a playlist (the callibration set) as the input, and attempts to recover the remaining 30% of the songs (withheld set) from the playlist as recommendations. These are made my distinguishing songs as belonging to the playlist or not - a binary classification task. To fit the model, we have data from a training set of complete playlists.
The appropriate methodology to perform this task using scikit-learn would be to use the MultinomialNB class. However, this would add needless complexity and prevent us from entirely using our domain knowledge correctly. For instance, we know that the order of the songs in a given playlist is not relevant in both the calibration set and the withheld set . Further, the size of a playlist can vary, making the construction of the design matrix more complicated. The common solution employed in such scenarios: a one-hot encoding of the categorical input data is practically comlpetely infeasible given the data dimesnions (~50k songs, >100 songs per playlist).
Keeping these constraints in mind, and with the goal of producing an implementation tailored to this particular use-case that can be optimised further for speed in the future, we chose to design a naive Bayes classifier from scratch.
Internal Model Representation
The naive Bayes model essentially relies on the estimation, storage, and finally the utilisation of one probability for each pair of songs, where the first belongs to the calibration set and the second belongs to the the withheld set . To represent this, our implementation uses a dense numpy matrix X of size N * N, where N is the total number of unique songs in the dataset. Each element of the matrix X(i,j) represents the probability that song j belongs to the withheld set if song i belongs to the calibration set. Since we know that the order of the songs in the playlist can be shuffled without any effects on the recommendations, we can constrain the constructed matrix X to be symmetric. That is to say, that the occurence of any two songs i and j in the same playlist in the training set implies that both the X(i,j) entry and the X(j,i) need to be modified. This is in contrast to typical model fitting techniques, which would split each training playlist into a callibration set and a witheld set, and make an update for say X(i,j) only when i was in the callibration set and j in the withheld set.
Model Fitting
To train the model we wish to find an X matrix that reflect the playlists comprising training set. Note that an empty training set would reflect in a matrix X where every element would be zero. Thus, we first initialise the matrix this way (equal to zero), and then make sequential updates to the probability estimates. We iterate through all the playlists, and search for every possible pair (i,j) of songs. For each pair we encounter, we make two updates to the matrix: we increment the values at X(i,j) and X(j,i). Finally, we implement the Laplace smoothing prior common in naive Bayes literature (and coincidentially also the default setting in scikit-learn’s MultinomialNB class)
Prediction
Given a calibration set, we can find corresponding rows for each track in our matrix X. Summing these up, we get a single row vector with one element corresponding to each song. We interpret these to be proportional to the probability of each track being in the withheld set. To recommned a set of say n songs, we simply select the songs with the largest n values in this array. It is noteworthy that prediction with this model consists of only lookups of the matrix X, and addition operation, and finally a top-n search. Pairwise distance computations - extremely common in recommender systems, are not involved at all.
Performance
We have identified the three metrics (RPS, NDCG and hit-rate) to evaluate our model. To obtain the final metrics, we compute the mean of the scores across all the playlists in the test set, across different values for number of recommendations.
Below the histograms show a distribution of the scores across the three different metrics, with two distributions for RPS and NDCG, one each for the case where the number of recommendations equals the number of songs used for calibration and where it equals the number of withheld songs.
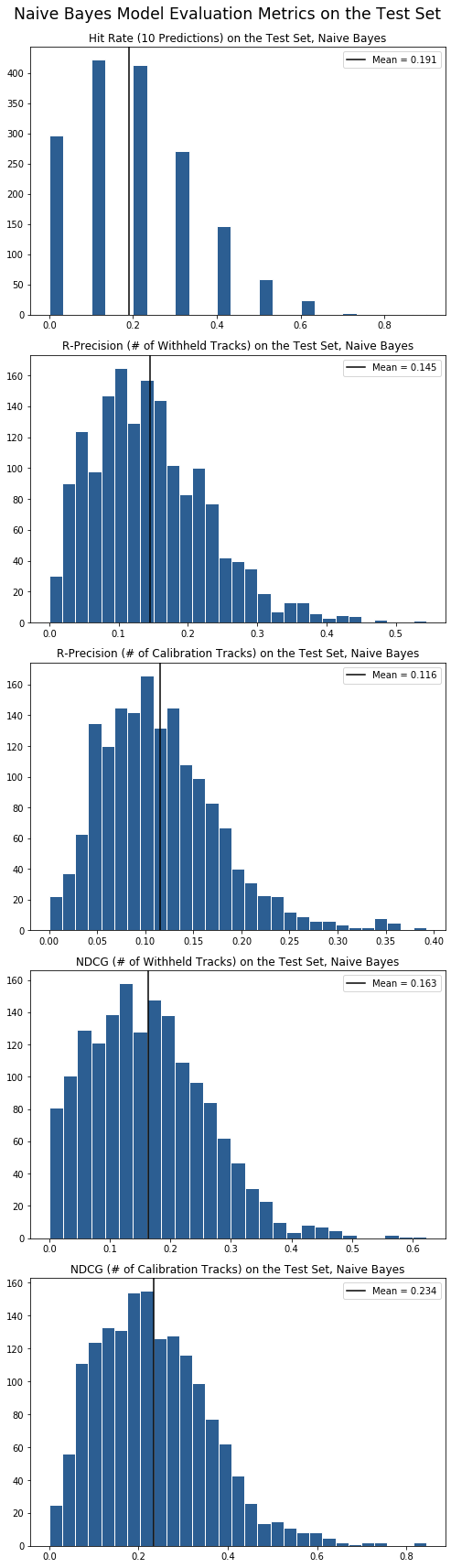
Overall, with 50 neighbors, the naive Bayes model achieved a 0.116 R-precision score and 0.234 NDCG score by producing the same number of recommendations as the number of songs used to calibrate the model. The R-precision score of 0.116 implies that if given a list of 100 songs, the model is able to produce 100 songs, out of which 11.6 on average would be songs that were in the withheld list of songs.